経緯

後輩から以下のようなLINEがきました。

「適切」という言葉が曖昧だが、以下のように解釈しました。

1. 材料の本数が最小であること。
2. 最後、余る棒の長さが最大であること。

要は、あまり材料を使わず、しかも、あまりを使いまわせるように出来る限り、長く取ろうという話。

とりあえず、俺なりの回答

Rubyで総当りのプログラムを作りました。ちょっと無駄は多いけど、まぁ、ひとまず動くのでいいかなと思います。

L = 6000
needs = {
  a: {length: 1322, num: 2},
  b: {length: 1264, num: 6},
  c: {length: 1283, num: 6}
}

def culc(require_list)
  sums = []

  require_list.each do |k, v|
    v[:num].times do |i|
      # 配列をコピーして、キーを追加
      added_sums = Marshal.load(Marshal.dump(sums))
      added_sums.map{|el| el << k }

      # もとの配列とキーを追加した配列を結合
      sums.concat added_sums

      # キー単体を追加
      sums << [k]

      # 定尺を超えた物を削除
      sums.delete_if{|x| x.inject(0) {|sum, n| sum + require_list[n][:length]} > L}

      # 重複を削除
      sums.uniq!
    end
  end

  hashes = []
  sums.each do |nl|
    hashes << {pattern: nl, score: nl.inject(0) {|sum,n| sum + require_list[n][:length]}}
  end

  max_pattern = hashes.max{|a,b| a[:score] <=> b[:score]}
  p max_pattern

  max_pattern[:pattern].each do |item|
    require_list[item][:num] -= 1
  end

  require_list.delete_if{|k, v| v[:num] <= 0}

  if require_list.size > 0
    culc require_list
  end
end

puts "required list"
puts "====================================="
p needs
puts ""
puts "best combination"
puts "====================================="

culc needs

出力はこんなかんじ。

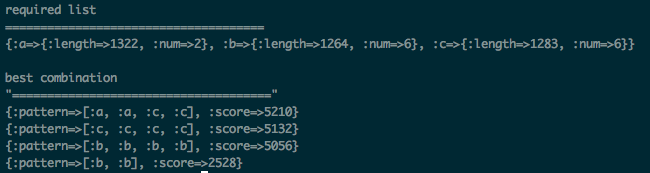
考察

この問題は部分和問題の類似問題かなーと思いました。

部分和問題とは、たとえば

[1,4,5,9]を適当に組み合わせて和が12になるようにできるか？

というような問題。この場合は、回答はNoです。どれだけ頑張っても12は作れません。

今回の問題はピッタリになることは通常ないと思うので、12以下の最大の値を作るためにはどうすればいいか？という話です。

たぶん、動的計画法に類似した方法になっているのかなーと思います。